Bakery mutual exclusion algorithm:
bakery : SYSTEM
BEGIN
comp1 : PROGRAM
y1 : VAR nat WHERE y1=0
BEGIN
WHILETRUE DO
y1 ::= y2 + 1 ;;
AWAIT y2 = 0 or y1 <= y2 ;;
y1 ::= 0
OD
END comp1
||
comp2 : PROGRAM
y2 : VAR nat WHERE y2=0
BEGIN
WHILETRUE DO
y2 ::= y1 + 1 ;;
AWAIT y1 = 0 or y2 < y1 ;;
y2 ::= 0
OD
END comp2
END bakery
This system is translated automatically into the following transition system:
bakery: SYSTEM
BEGIN
comp1 : PROGRAM
BEGIN
y1 : VAR nat
BEGIN
"Req_1"
1:: TRUE ---> y1 ::= y2 + 1
GOTO 2 []
"In_1"
2:: y2 = 0 or y1 <= y2 ---> GOTO 3 []
"Out_1"
3:: TRUE ---> y1 ::= 0
GOTO 1 []
END
END comp1
||
comp2 : PROGRAM
BEGIN
y2 : VAR nat
BEGIN
"Req_2"
1:: TRUE ---> y2 ::= y1 + 1
GOTO 2 []
"In_2"
2:: y1 = 0 or y2 < y1 ---> GOTO 3 []
"Out_2"
3:: TRUE ---> y2 ::= 0
GOTO 1 []
END
END comp2
INITIALLY :
y1 = 0 and y2 = 0 and pc2 = 1 and pc1 = 1
END bakery
The property we want to prove is
not (pc1=3 and pc2=3)
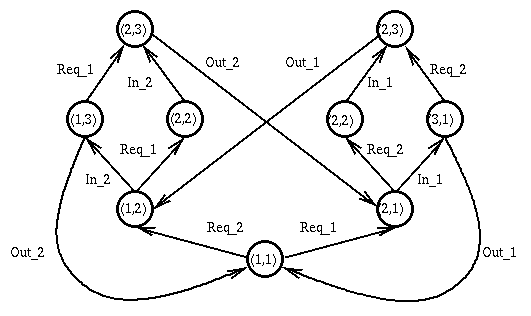
The following abstract state graph is constructed for the bakery system using
the predicate: y1 = 0, y2 = 0, y2 < y1 and y1 <= y2.
The control configuration (3,3) which violate mutual exlusion
property is not reachable.
Back to the Invariant Checker home page
